Secção 1.2 - Teoria clássica da Radiação de Cavidade de Rayleigh - Jeans

No início do século XX, John Rayleigh (1842-1919) e James Jeans (1877-1946), utilizaram a teoria clássica para estudar a densidade de energia da radiação de cavidade, ou de corpo negro, que resultou em sérias divergências com resultados experimentais. Estas divergências revelam-se como uns dos fatos históricos mais importantes para o nascimento da teoria quântica. Nesta secção, vamos apresentar os cálculos feitos por Rayleigh e Jeans e discutir as divergências observadas. Na secção seguinte, discutiremos a teoria de Planck para a radiação de cavidade, que introduziu a quantização da energia.

Se as paredes internas da cavidade da fig.(1.1), estiverem uniformemente aquecidas a uma temperatura T, o orifício atua como um emissor de radiação, como mostra a fig. (1.3).

Fig. 1.3 - cavidade uniformemente aquecida emissora de radiação

Como o orifício tem propriedade de uma superfície de corpo negro, a radiação emitida por ele deve também ter um espectro de Corpo Negro. O espectro emitido pelo orifício na cavidade será especificado também por uma radiância espectral R_T (ν). No entanto, é mais útil, especificar o espectro da radiação dentro da cavidade, conhecida como radiação de cavidade, em termos de uma densidade de energia ϱ_T (ν). Evidentemente, essas quantidades são proporcionais entre si.
A relação entre a radiância R_T e a densidade de energia ϱ_T, pode ser encontrada com a ajuda de uma esfera imaginária com o orifício da cavidade em sua superfície, como mostra a fig.(1.4).

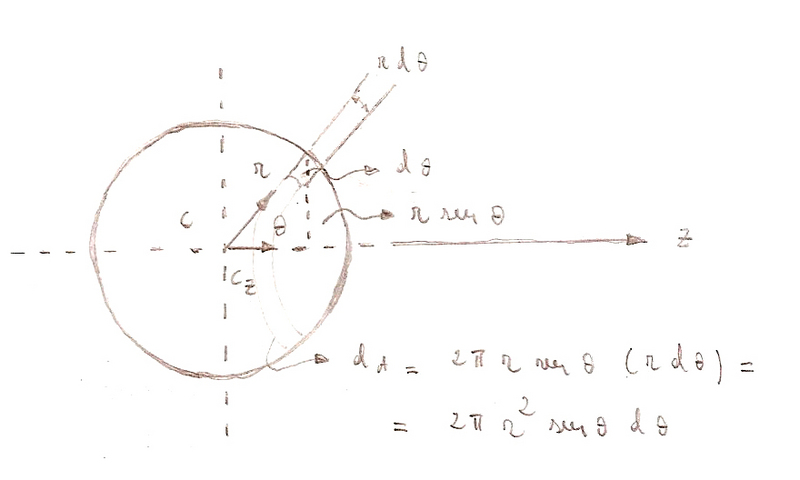
Fig.(1.4) - Esfera imaginária com orifício da cavidade.

Devemos notar que, como somente um dos hemisférios dA contém o orifício, então num intervalo de tempo ∆t, a energia radiada ∆E_R será metade da energia ∆E_C da cavidade. Além disso, somente radiação com cavidade Z> atravessam o furo. Evidentemente, a média Z> pode ser ponderada em qualquer intervalo do hemisfério [ - π/2 , π/2 ]. Em particular, pode-se ponderá-la no octante [0, π/2]. Com essas considerações, obtém-se:

R_T = ∆Ec/∆t . 1/∆A . (<∆z>)/(<∆z>) = 1/2 Z> ∆Ec/∆V = 1/2 Z> ϱT

com,Z> ponderada na área da semi- esfera:

Z>= (∫_0^(π/2) (c cosθ)2πr² senθ dθ)/(∫_0^(π/2) (2πr² sen θ dθ) = (2πr² c)  ∫_1^0 (x d x)/(2πr²) ∫_1^0 dx) = c/2

onde, adotou-se a mudança de variável x = cos θ. Assim, a radiância e a densidade de energia na cavidade se relacionam por,

R_T = c/4 ϱT

ou, num intervalo de freqüências entre ν e ν + dν,

R_T (ν)dν = c/4 ϱT (ν) dν (1.10)

ou ainda, em termos de comprimento de onda,

R_T (λ) dλ = c/4 ϱT (λ) dλ (1.11)

pois, como c = λν , dν/dλ =  -c /λ² , e portanto dν é proporcional a - dλ . Pode-se considerar as paredes internas da cavidade perfeitamente condutora, tal que, os campos sejam confinados, e que a energia seja armazenada na forma de ondas eletromagnéticas estacionárias de modos discretos para qualquer freqüência ν. Podemos então, determinar a densidade de energia espectral ϱT (ν) d(ν) num intervalo de freqüência entre ν e ν + dν, simplesmente contando o número de modos N (ν) dν no mesmo intervalo de freqüências e multiplicando pela energia total média <ℇ> de cada modo:

ϱ_T (ν) d(ν) = (N(ν)d(ν))/V < ℇ > (1.12)

onde, V é o volume da cavidade. O problema se reduz então na determinação dos fatores N (ν) d(ν) e < ℇ >.

Para simplificação matemática na determinação de N(ν) d(ν), assumiremos que a forma da cavidade seja cúbica de dimensões L, como mostra a fig.(1.5). Nesse caso, as componentes dos  vetores campos elétricos E e magnético B, podem ser tratadas separadamente, por causa do paralelismo das paredes.

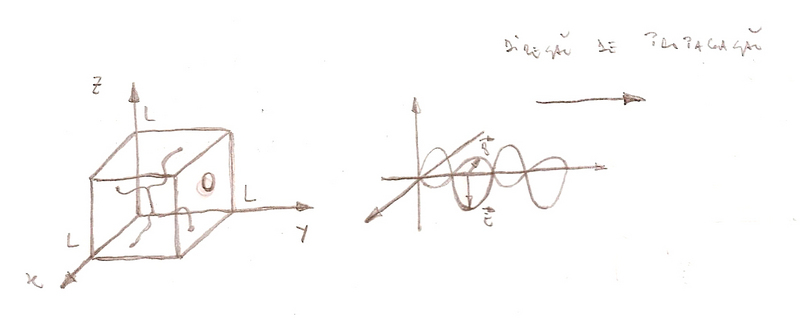
Fig.(1.5) - Cavidade cúbica perfeitamente condutora.

A radiação eletromagnética é uma vibração transversal, com vetores E  e B perpendiculares à direção de propagação como também mostrado na fig.(1.5).

O comportamento espacial e temporal dos campos E e B é obtido através das equações de J. C. Maxwell (1871-1879). Entretanto, por causa da natureza vetorial desses campos, o tratamento matemático envolvido na solução geral do problema é bastante tedioso. Ao invés de fazê-lo, vamos optar inicialmente, por resolver uma situação hipotética simplificada, onde a cavidade seja unidimensional de comprimento L, de modo que a natureza vetorial dos campos possam ser ignoradas. Uma vez resolvido este problema simples, vamos generalizá-lo ao caso tridimensional utilizando argumentos geométricos simples.

Ao longo do eixo-x, os campos E (x, t) e B (x, t), satisfazem a equação de onda semelhantes ao caso de cordas vibrantes presas pelas extremidades, isto é,

(∂² E(x, t))/∂x² = (1/c²) (∂² E(x,t))/∂t² (1.13)

e uma equação similar para B (x, t); que não será explicitada aqui. Nesta equação c = λν, é a velocidade da luz (c = 3,00 x 108 m/s). A solução da equação (1.13) para uma onda estacionária (resultante da soma de onda para direita e esquerda), será:

E (x, t) = E₀ [sen (kx + wt) + sen (kx - wt)] = E₀ sen kx sen wt (1.14)

onde,

k = 2π/λ e, w = 2πν (1.15)

são, respectivamente, o numero de ondas e a freqüência angular. A identidade na equação (1.14) pode ser verificada usando-se a relação, sen α + sen β = 2 sen 1/2 (α+ β) cos 1/2 (α-β).
A equação (1.14), descreve o comportamento de uma onda cuja amplitude varia senoidalmente, no espaço e no tempo, ao longo do eixo-x e com freqüência ν. Esse comportamento deve ser espacialmente localizado, como ondas estacionárias, exibindo nódos em x= 0 e x = L. Para que o campo E (x, t) seja nulo nesses pontos, de acordo com a equação (1.14), sen (2πL/λ) = 0, ou 2πL/λ = nπ onde, n = 0, 1, 2,..., ou seja, o comprimento de onda λ deve assumir valores dados por,

λ = 2L/n ; n = 0, 1, 2, ... (1.16)

ou ainda, em termos de freqüência,

ν= c/λ = c/2L n; n = 0, 1, 2,... (1.17)

Esta condição determina um conjunto de valores possíveis de comprimentos de onda, ou freqüências, que devem se propagar na cavidade unidimensional. A figura (1.16) mostra ondas estacionárias para n = 1, 2, 3.

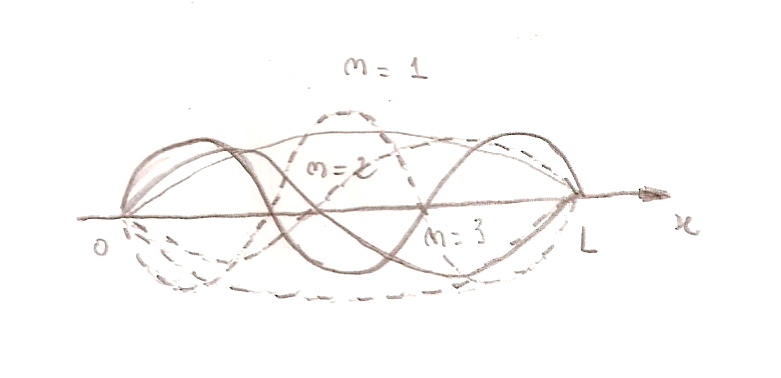
Fig.(1.6) - Ondas estacionárias para n = 1, 2 e 3.

Um comportamento similar se obtêm quando se considera as dimensões y e z individualmente, isto é, as radiações se propagam de modo que suas três componentes espaciais são ondas estacionárias.
Para generalizar o problema ao caso tridimensional, consideremos uma radiação de comprimento de onda λ, propagando-se numa direção definida pelos três ângulos diretores α, β e γ, como mostra a figura (1.7). Obviamente, as radiações devem ser ondas estacionárias já que suas componentes espaciais o são e, neste caso, os nodos são planos distanciados de λ/ 2.

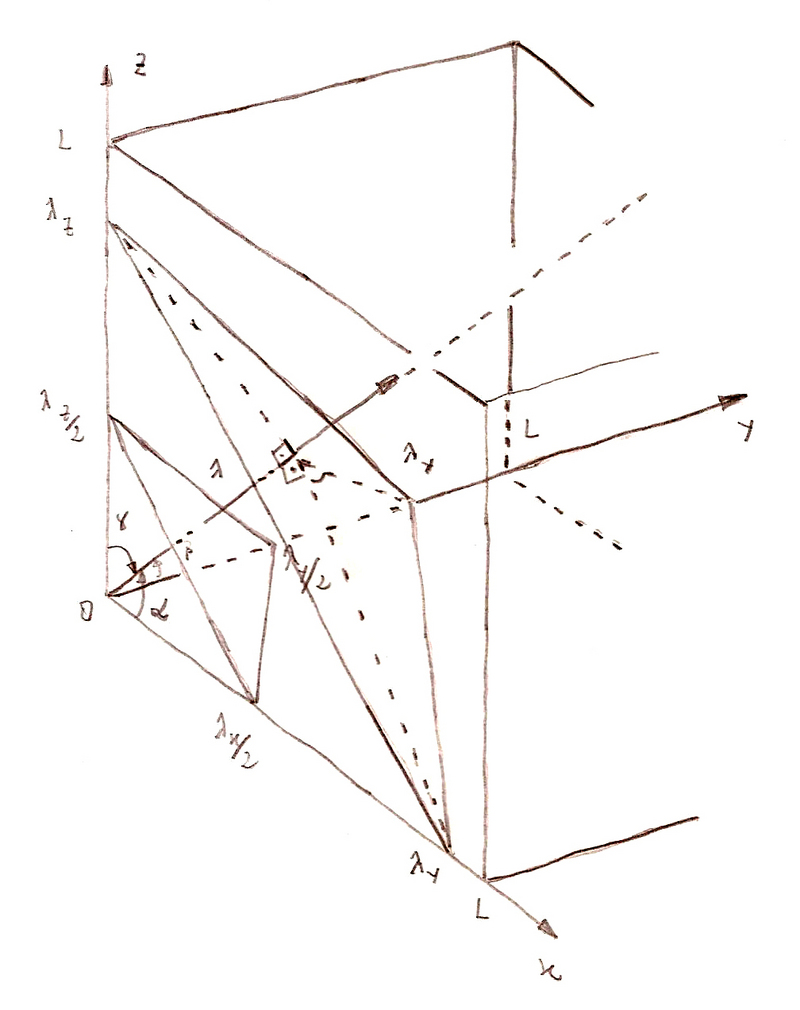
Fig.(1.7) - Planos nodais que se propagam numa certa direção na cavidade cúbica.

Como na equação (1.16) os comprimentos de onda associados a cada coordenada espacial, serão,

λx = 2L/ nx; λy = 2L/ ny ; λz = 2L/ nz (1.18)

onde, nx , ny , nz = 0, 1, 2, ... . Estas componentes podem ser escritas em termos do comprimento de onda λ, como sugere a figura (1.7),

cos α = λ/ λx ; cos β = λ/ λy ; cos γ = λ/ λz (1.19)

que relacionadas com as equações (1.18), fornecem,

2L/λ cos α = nx ; 2L/λ cos β = ny ; 2L/λ cos γ = nz

Elevando-se ambos os membros destas equações ao quadrado e, em seguida somando-os, obtemos

(2L/λ)² (cos² α + cos² β + cos² γ) = nx² + ny² + nz²

O segundo termo entre parênteses, define a soma dos co-senos diretores dada por,

cos² α + cos² β + cos² γ = 1 (1.20)

e, então,

2L/λ = (nx² + ny² + nz²)^1/2; nx, ny, nz = 0, 1, 2, ... (1.21)

Em termos de freqüência, a equação (1.21) pode ser escrita como,

ν = c/λ = c/2L (nx² + ny²+ nz²); nz , ny , nz = 0, 1, 2, ... (1.22)

Essas equações descrevem novamente um conjunto de valores possíveis de comprimento de onda e freqüência, agora para o caso geral da cavidade cúbica condutora.
Vamos agora contar o número de modos N (ν) dν, no intervalo de freqüência entre ν e ν + dν, construindo uma esfera de raio

r = (nx² + ny² + nz²)^1/2 (1.23)

em coordenadas retangulares, tal que o conjunto de inteiros nx , ny e nz definem pontos no interior de um octante do sistema de coordenadas, fig. (1.8).

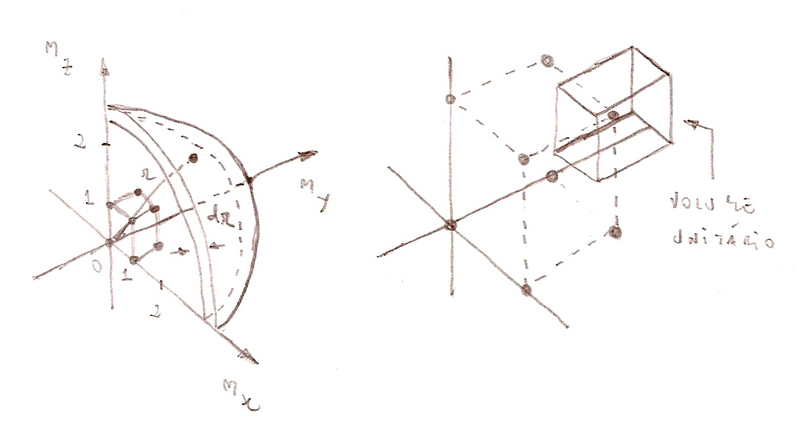
Fig.(1.8) - Espaço (nx, ny , nz ) definindo um octante esférico de raio r = (nx² + ny² + nz²)^1/2.

O volume total do octante esférico pode ser dividido em volumes unitários, contendo cada um, apenas um ponto (nx, ny , nz). Esta construção permite definir a densidade de pontos como,

ϱ = 1 ponto/ unidade de volume (1.24)

Cada ponto (nx, ny, nz ) corresponde a uma freqüência possível ν, que se relaciona ao raio r, de acordo com as equações (1.22) e (1.23), como

r = (2L/c) ν (1.25)

Assim, calcular o número de modos N (ν)dν entre ν e ν + d ν, é equivalente a calcular o número de pontos N (r) dr, contidos entre as cascas esféricas entre r e r + dr. O valor de N (r) dr pode ser calculado simplesmente, multiplicando o volume da camada entre r e r + dr pela densidade de pontos, isto é,

N (ν) dν = N (r) dr = (1/8 4πr²) dr ϱ = (1/2πr²) dr

pois, ϱ = 1. Utilizando a equação (1.25) e sua derivada, dr = (2L/c) dν, na equação anterior obtém-se:

N (ν) dν = ½ π ( 2L/c ν)² ( 2L/c) dν = (4πν²/c³) V dν (1.26)

onde, usamos o volume da cavidade como, V = L³.

Finalmente, devemos multiplicar o resultado da equação (1.26) por um fator 2, pois, para cada freqüência possível ν, há, na verdade, duas ondas independentes correspondentes aos dois possíveis estados de polarização da radiação eletromagnética, que podem estar ou não em fase, isto é,

N (ν) dν = (8πV/c³) ν² dν (1.27)

Apesar de nossos cálculos terem sido feitos para uma cavidade, pode-se mostrar que N (ν) depende apenas do volume da cavidade e não de sua forma.
Relacionando-se a equação (1.27) com a equação (1.12), obtém-se:

ϱ_T (ν) dν = (8πν²/c³) <ℇ> dν (1.28)

Classicamente, as ondas estacionárias de freqüência ν são geradas por oscilações de partículas carregadas das paredes da cavidade, como se fossem pequenos corpos presos a molas, mantidos em equilíbrio térmico a uma temperatura T.
Baseando-se no modelo clássico da teoria cinética dos gases, na qual um sistema de moléculas em equilíbrio térmico a uma temperatura T, o princípio da eqüipartição da energia, afirma que a energia cinética média de uma molécula por grau de liberdade é,

1/2 KT

onde, K = 1,38 x10^-23 J/ k, é a constante de Boltzmann.

Podemos aplicar este princípio à partículas oscilantes das paredes da cavidade desde que consideremos também a energia potencial dessas partículas. No equilíbrio térmico, em média, as contribuições da energia cinética e potencial para a energia total, são iguais a 1/2 KT. Logo, nessas condições, a energia total média será KT. No nosso caso, as ondas estacionárias tem somente um grau de liberdade dada pela direção da oscilação das partículas, associadas ás vibrações transversais do campo E da onda estacionária. Conclui-se, portanto, que cada onda estacionária tem energia total média,

<ℇ> = KT (1.29)

é importante notar que a energia total média tem o mesmo valor para todas as ondas estacionárias na cavidade, independentemente de suas freqüências.

Substituindo-se a equação (1.29) na equação (1.28), obtém-se a densidade de energia no intervalo de freqüência entre ν e ν + dν, de acordo com previsões clássicas:

ρ_T (ν) dν = (8Πν² KT/ c³)  dν ( 1.30)

Esta relação é conhecida como a fórmula de Rayleigh-Jeans para radiação de corpo negro.
A fig.(1.9) mostra o comportamento da equação (1.30), e o resultado experimental. A discordância é evidente. O espectro clássico se aproxima dos resultados experimentais, somente no limite de baixas freqüências. A medida que a freqüência cresce, o resultado teórico tende ao infinito.

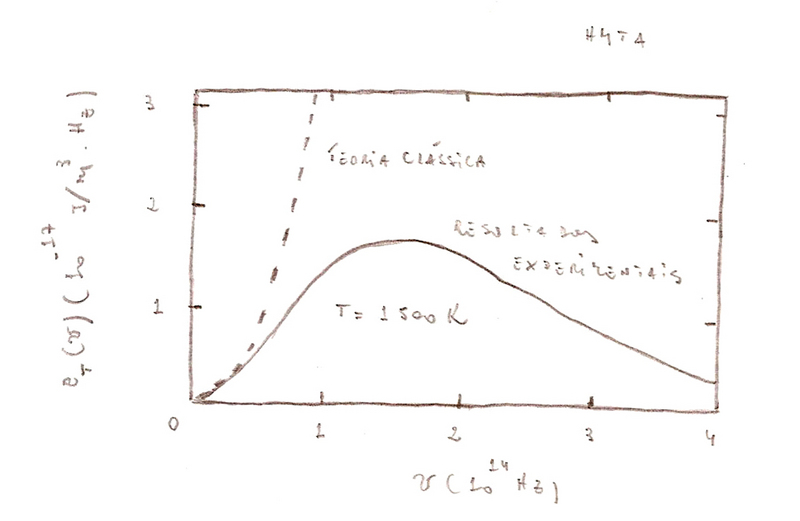
Fig.(1.9) - Resultado de Rayleigh - Jeans para a radiação de um corpo negro comparado com os resultados experimentais.

A tendência ao infinito para altas freqüências na teoria de Rayleigh - Jeans, é conhecido como catástrofe do ultravioleta. A experiência mostra que, na realidade, a densidade de energia vai a zero para altas freqüências.
O problema da radiação de cavidade foi resolvido por Planck, assumindo uma hipótese sobre a eqüipartição da energia até então desconhecida. Na secção seguinte vamos discutir essas idéias e mostrar sua importância para o surgimento da física quântica.