Secção 1.3 - Teoria de Planck da Radiação de Cavidade
Na tentativa de solucionar a discordância entre a teoria clássica e a experiência, para a radiação de cavidade, Planck considerou uma hipótese que violava o princípio da eqüipartição da energia. Planck observou que o resultado experimental seria reproduzido quando,
lim <ℇ> = KT e, lim <ℇ> = 0 (1.31)
ν→0 ν→∞
isto é, a energia total média tende a KT, como na teoria clássica, quando a freqüência tende a zero, mas tende a zero quando a freqüência tende a infinito. Assim, Planck supõe que a energia média das ondas estacionárias seja uma função da freqüência <ℇ> = <ℇ (ν)>, contradizendo o princípio da equipartição da energia.
O princípio da equipartição da energia, tem a sua origem na distribuição de Boltzmann, para a teoria cinética clássica. A distribuição de Boltzmann dá a probabilidade de encontrar um sistema físico, em equilíbrio térmico a uma temperatura T, com energia entre ℇ e ℇ + dℇ, escrita aqui sem demonstração, como,
P (ℇ) dℇ = (e^ (-ℇ/KT)/(KT) dℇ (1.32)
A energia média <ℇ> pode ser calculada da distribuição de Boltzmann por,
< ℇ > = (∫_0^∞ (ℇ P(ℇ)dℇ)/(∫_0^∞ P(ℇ)dℇ) = ∫_0^∞ (ℇ P(ℇ)dℇ) = ÁREA (1.33)
O denominador é a probabilidade de encontrar a entidade com qualquer energia, sendo portanto igual a unidade. A integral na equação (1.33) pode ser calculada utilizando a equação (1.32), e o resultado reproduz o princípio da equipartiação da energia, isto é,
<ℇ > = KT (1.34)
A equação (1.33) mostra que <ℇ> = KT é representado pela área abaixo do gráfico de ℇ P(ℇ) em função de ℇ, como mostra a fig. (1.10). A função ℇ P(ℇ) foi obtida diretamente da equação (1.32). O ponto de máximo desta função corresponde a ℇ = KT = <ℇ>.
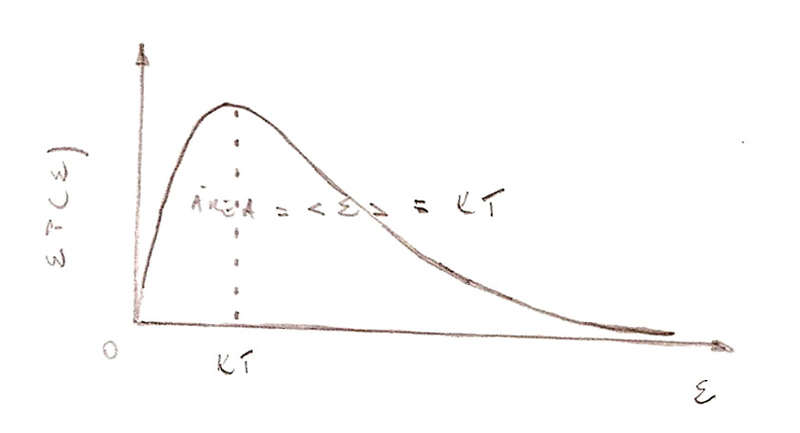
Fig. (1.10) - Gráfico de ℇ P(ℇ) em função de ℇ.
A grande contribuição de Planck se deu quando ele descobriu que a condição lim <ℇ> = 0, poderia ser alcançada, se fosse modificado o cálculo de <ℇ> a partir de P(ℇ) dℇ. Planck supôs que a energia ℇ poderia ter apenas valores discretos, em vez de qualquer valor como utilizado na teoria clássica, e que, os valores discretos fossem uniformemente distribuídos, isto é,
ℇ = 0, ∆ℇ, 2∆ℇ, 3∆ℇ, ... (1.35)
Nesse caso, ∆ℇ seria o intervalo constante entre os valores discretos da energia. Com a hipótese discreta da energia, as integrais na equação (1.33), usadas para calcular <ℇ>, devem ser substituídas por somatórios, isto é,
<ℇ> = (∑_0^∞ [ℇn P(ℇn)])/(∑_0^∞ [P(ℇn)]) (1.36)
A fig.(1.11) mostra cálculos gráficos de <ℇ> a partir de ℇ P(ℇ) para os casos, (a) ∆ℇ <<< KT; (b) ∆ℇ ≈KT e (c) ∆ℇ >> KT.
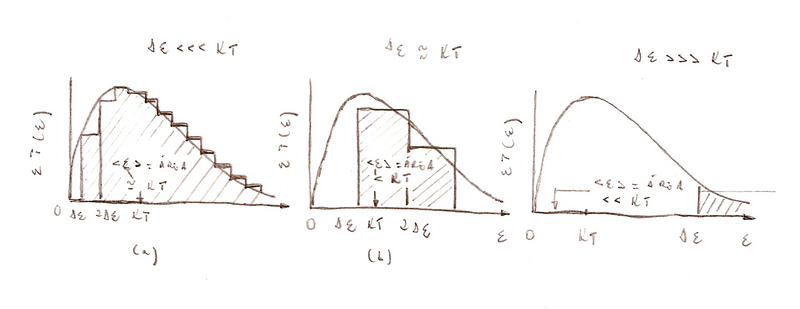
Fig.(1.11) - Comportamento gráfico de <ℇ> de acordo com a equação (1.36).
O valor de KT será a área abaixo da curva suave. Observe que quando ∆ℇ <<< KT, o valor de <ℇ> ≈ KT, ou seja, praticamente igual ao resultado clássico. Entretanto, quando <ℇ> ≈ KT ou, ∆ℇ >> KT, o valor <ℇ> será menor que KT, pois a redução da área definida pelos elementos discretos começa a tornar-se evidente, quando comparamos com área definida pelos contínuos. Conclui-se então que:
<ℇ> ≅KT se, ∆ℇ for pequeno
e,
<ℇ> ≅0 se, ∆ℇ for grande
Como Pkanck precisava obter o primeiro resultado para baixas freqüência ν, e o segundo para altos valores de ν, então o valor ∆ℇ deveria ser proporcional a ν, isto é,
∆ℇ = hν (1.37)
onde, h é a constante de proporcionalidade. Cálculos posteriores ∞permitiram a Planck determinar o valor de h, ajustando resultados teóricos com dados experimentais, obtendo,
h = 6,63 x 10-34 J.s (1.38)
Esta constante ficou conhecida como a constante de Planck.
Vamos agora calcular a energia média utilizando a equação (1.36) e equação (1.32), considerando nessas fórmulas a energia
ℇ = nhν, n = 0, 1, 2, 3, ... (1.39)
isto é,
<ℇ> = (∑_ 0^∞ (nhν/KT) e^ (- nhν/KT) )/(∑_0^∞ (1/(K ) e^(-nhν/KT) ) = KT (∑_0^∞ [nα e^(-nα)])/(∑_0^∞ e^(-nα) )
onde,
α = hν/KT (1.40)
podemos notar que,
-α (d/dα) ln∑_0^∞ e^(-nα) = (-α (d/dα) ∑_0^∞ e^(-nα) )/(∑_0^∞ e^(-nα) ) = (-∑_0^∞ [α (d/dα) e^(-nα)])/(∑_0^∞ e^(-nα) ) = (∑_0^ ∞ nαe^(-nh) )/(∑_0^∞ e^(-nα) )
de forma que,
<ℇ> = KT ( -α (d/dα) ln ∑_0^∞ e^(-nα) ) = - hν (d/dα) ln ∑_0^∞ e^(-nα)
onde usamos o valor de dado por (1.40). Mas,
∑_0^∞ e^(-nα) = 1 + e^(-α)+ e^(-2α)+ e^(-3α)+ ...= 1+x+x² + x³ + ... = (1- x) -1
onde, x = e^(-α), de forma que,
<ℇ> = -hν (d/dα) ln ( 1- e^(-α))-1 = (-hν)/((1- e^(-α) )-¹) (-1) ( 1 - e^(-α))-2 e^(-α) = (hνe^(-α))/(1-e^(-α) ) = hν/(e^α - 1)
ou,
<ℇ> = hν/[e^(hν/KT)-1] (1.41)
Substituindo-se a equação (1.41) na equação (1.28), obtém-se a densidade de energia no intervalo de freqüências entre ν e ν + dν, de acordo com a previsão quântica de Planck:
ϱT (ν) dν = [(8π ν²)/c³] [hν/(e^(hν/KT)-1)] dν (1.42)
que descreve o espectro de corpo negro de Planck.
Este resultado está em perfeita concordância com resultados experimentais.
Em muitos casos, é conveniente expressarmos o espectro de corpo negro de Planck em termos de comprimentos de onda λ em vez de freqüência ν. Como dν e dλ tem sinais opostos, de forma que
ϱT (λ) dλ = - ϱT (ν) dν
ou,
ϱT (λ) = - ϱT (ν) dν/dλ = ϱT (ν) c/λ² (1.43)
pois, como c = λν, dν/ dλ = -c / λ².
Substituindo-se a equação (1.42), sem dν, na equação (1.43), em seguida escrevendo ν = c/ λ, e multiplicando ambos os lados por dλ, obtemos,
ϱT (λ) dλ = (8πhc/ λ5) (dλ / [e^(hc/λKT)-1] (1.44)
A fig. (1.12) mostra gráficos do espectro de Planck, em termos de comprimento de onda λ, para diferentes valores de temperatura T.
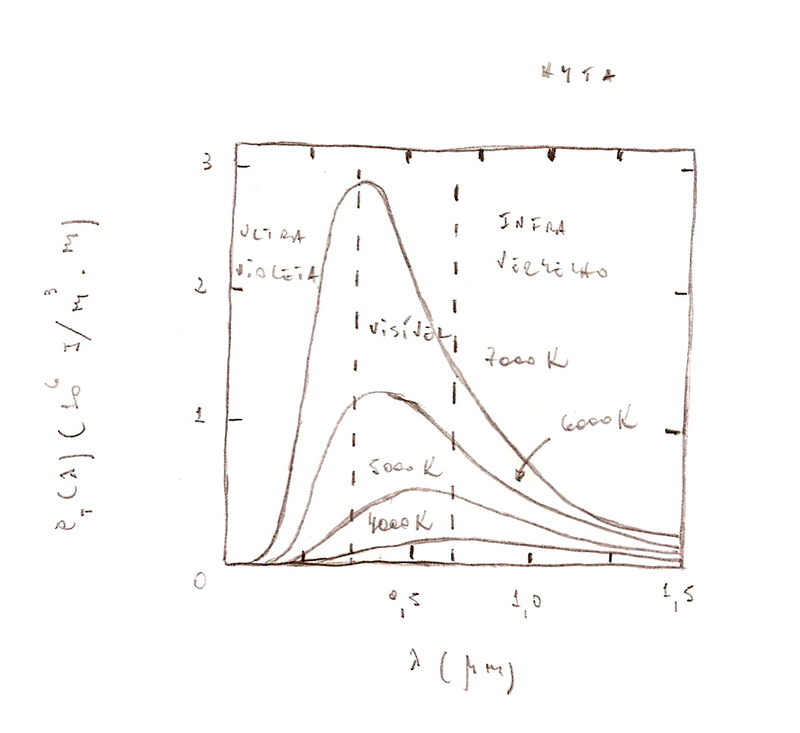
Fig.(1.12) - Espectro de corpo negro de acordo com Planck.
A mudança de "cor vermelha" para "cor azul" da radiação térmica, à medida que a temperatura sobe, torna-se evidente na fig.(1.12), com o deslocamento dos máximos dos espectros para a esquerda.
A lei de Stefan - Boltzmann equação (1.2), e a lei do deslocamento de Wien (equação 1.9), podem ser obtidas a partir da fórmula de Planck.
A lei de Stefan-Boltzmann é obtida integrando-se a lei de Planck sobre todo o espectro de comprimento de onda. A lei do deslocamento de Wien pode ser obtida fazendo-se
dϱT (λ)/ dλ = 0 (1.45)
o resultado encontrado deve ser,
λmáx . T = hc/(4,965 K) (1.46)
Identificando o lado direito desta equação com a constante de Wien, determinada experimentalmente como sendo 2, 898 x 10-3 m . k, e utilizando c = 3,00 x 10-8 m /s, pode-se encontrar uma relação entre h e K. Isto foi feito por Planck, e os resultados obtidos estão em ótima concordância com valores posteriormente encontrados por outros métodos.
Exemplo 1.2
Obtenha a lei de Stefan-Boltzmann à partir da fórmula de Planck da radiação de corpo negro.
Solução
A radiância RT (ν) e a densidade de energia ϱT (ν), no intervalo de freqüência entre ν e ν + dν, é dada pela equação (1.11), que relacionada com a fórmula de Planck (equação 1.42), resulta em,
RT (ν) dν = c/4 ϱT (ν) dν = (2πh/c²) [ν³/(e^(hν/KT)-1)] dν
A radiância total, será
RT = ∫_0^∞ RT (ν) dν = 2πh/c² ∫_0^∞ (ν³dν) /(e^(hν/KT )-1) = (2πh/c²) (KT/h)4 ∫_0^∞ (α^3 dα)/(e^α-1)
onde, usa-se a mudança de variável,
α= hν/KT ⇒ ν = (KT/h) α
Numa tabela de integrais, encontra-se:
∫_0^∞ (α³ dα)/(e^α-1) = π5 / 15
assim,
RT = σ T4
onde,
σ = 2π5k4/ 15h³c² = 5,676 x 10-8 w/ m²k4
Que está em excelente concordância com o valor da constante obtida por Stefan-Boltzmann.